Web系エンジニアのアウトプット練習場

エンジニアリングと書評が中心。たまに全然関係無い話もします。
トップページ/画像処理/金属製品のメッキ不良を自動で検出するためには？/
2018年02月21日

金属製品のメッキ不良を自動で検出するためには？

画像処理

前置き

近年の製造業は、ラインの自動化により人手がいらなくなると言われています。
ただし、一部の大企業のみラインの自動化を完成させていますが、本当に自動化が必要な人手不足の中小企業ではラインの自動化が実現できていない、というのが現状です。
とくに「自動検品」は製品によって使用も検査するポイントも異なり、基本的にはオーダーメイドとなるため、なかなか導入が難しい点です。
僕が所属している会社も金属端子を製造しているのですが、複数人による目視で何万個もの製品を検査しています。
僕も試しに目視での検品をやってみましたが、数百個で目が痛くなりました。
なんとしてもこの問題を早く低コストで解決せねばならない、そう思い、まずは簡単そうなメッキ不良検査について考えてみることにしました。

どういう方法で検品するか

以下の2つのアプローチを思いつきました。

  • Machine Learningによるアプローチ
  • 画像処理によるアプローチ

検品対象が１種類の製品だけであれば、機械学習アプローチでも良さそうですが、うちは多品種小ロット生産なので製品ごとにいちいちデータを集めて学習させるのはちと現実的ではなさそうです。
メッキ不良を見分けるだけなら、画像処理アプローチでも簡単にできそうなので、今回は画像処理によるアプローチを試してみることにします。
画像処理ライブラリとしてはOpenCVのPython版を使用することにしました。

どのカメラで検品する？

まずは、手元にあったWebカメラをPCにつないで試しました。
結果から言うとうまくいきませんでした。

うまく行かなかった点

  • 光が乱反射して被写体全体が白く光ってしまい、不良が確認できない
    • 金属は光の反射率が大きいため、適切に照明設定を行う必要がある
  • 画像が荒すぎる
  • AWB(オートホワイトバランス)などの自動調節機能が働いてしまう
    • 綺麗な動画を撮るのには便利だが、検品においては「被写体がきれいに映るよう最適化する」機能は邪魔でしかない

解決方針

上記の問題はすべて検品に使う機材を変更することで対応できそうです。

光の乱反射対応

外部からの光を遮断し、「同軸落射照明」を使用して試してみます。
同軸落射照明は直線的に光を入射し、光の反射のうち直線的に跳ね返ってきた光のみを受け取ります。
詳しい原理はご自身でググってください。

画像が荒すぎる、自動調節機能が邪魔

カメラをWebカメラから検品用のものに変えます。

選定した機材

これらの解決指針を踏まえてミスミやモノタロウなどで機材を揃えました。

  • L-835(高解像度USBカメラ)
  • L-802-2(カメラレンズ)
  • L-509(カメラ固定用ホルダー)
  • L-715(同軸落射照明)
  • AB5201(カメラ固定用支柱)
  • JB-203(挟み込み式パイプスタンド、AB5201を挿します)
  • CTM-A4G(カッティングマット、背景に使用します)

これらを組み合わせると↓みたいになりました。

手作り感に溢れる検品装置

手作り感に溢れる検品装置

画像処理方法

機材が揃ったところで画像処理の方法を考えていきます。

画像から検体のみを抽出する

案1: 画像を二値化して白い部分を抜き出す

OpenCVでは画像を二値化する関数が用意されています。

import cv2
src = cv2.imread('hoge.jpg')
gray = cv2.cvtColor(src, cv2.COLOR_BGR2GRAY)
ret, bw = cv2.threshold(gray, 100, 255, cv2.THRESH_BINARY)

まず、カメラからはカラー画像が得られるので、二値化がする前にcv2.cvtColorでグレースケール画像に変換します。
cv2.thresholdがグレースケール画像から二値画像を得る関数で、第4引数で二値化の方法を選択します。
上記の例では第2引数で指定する画素値を閾値として二値化する、cv2.THRESH_BINARYを渡しています。
得られた二値画像に対してオープニング・クロージングによるノイズ除去などを施して二値画像を出力してみましたが、検体のみをうまく抽出することはできませんでした。

  • 二値化を行うための適当な閾値が製品ごとに異なってしまう
  • そもそも不良がある場合、閾値を一意に決定することができない
  • 環境に左右されやすい

などの理由があります。

案2: 検体が写っている画像と背景画像の差分を抽出する(採用)

この方法はうまくいきました。
まず、以下のように背景画像のみを撮影しておきます。

背景画像

背景画像

続いて検体を乗せて差分を計算した後、差分が一定値以上の部分をマスクして検体のみを抜き出します。

# 読み込んだ画像とあらかじめ読み込んでおいた背景画像の差分を計算して二値化
diff = cv2.absdiff(src, self.background)
diff_gr = cv2.cvtColor(diff, cv2.COLOR_BGR2GRAY)
ret, diff_bw = cv2.threshold(diff_gr, 20, 255, cv2.THRESH_BINARY)

# オープニング・クロージングによるノイズ除去
element8 = np.array([[1, 1, 1], [1, 1, 1], [1, 1, 1]], np.uint8)
operator = np.ones((3, 3), np.uint8)
diff_md = cv2.dilate(diff_bw, operator, iterations=4)
diff_msk = cv2.erode(diff_md, operator, iterations=4)

# 元画像に差分がある部分だけマスクして抜き出す
dst = cv2.bitwise_and(src, src, mask=diff_msk)

検体のみを抽出

検体のみを抽出

良い感じに検体のみを抽出することができました。
あとはこれに対してメッキ不良を検出する画像処理を行います。

メッキ不良を検出する

案1: メッキ不良の色範囲を入力しておいてメッキ不良を抽出する

これはうまくいきませんでした。
しっかりとRGB値を図ってみると、似たようなメッキ不良でもRGB値の幅がかなり広く、良品の場合にも誤って検知してしまう場合がほとんどでした。

案2: 画像全体の色の平均を取って比較

これもうまくいきません。
理由は案1とあまり変わりません。

案3: 画像の画素値のヒストグラムを作成し、良品と不良品の比較を行う(採用)

あらかじめ良品画像の画素値のヒストグラムを作成しておき、不良品の画素値のヒストグラムとの類似度を求めます。
類似度の計算にはピアソンの積率相関係数(Pearson product-moment correlation coefficient)を使用しました。
ヒストグラムX, Yのピアソンの積率相関係は以下のように表されます。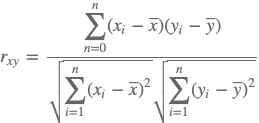

ピアソンの積率相関係

これによって単に画像の平均値や中央値を求めるよりもある程度細かく比較することができます。

ヒストグラムの作成

OpenCV

gray = cv2.cvtColor(src, cv2.COLOR_BGR2GRAY)
self.hist = cv2.calcHist([gray], [0], None, [256], [0,256])

ピアソンの積率相関係数を求める

numpyにピアソンの積率相関係数を求めてくれるメソッドがあります。

correlation = np.corrcoef(self.hist[20:240], self.good_hist[20:240], rowvar=False)

correlationは2x2の行列ですが、[[r_xx, r_xy], [r_yx, r_yy]]のようになっています。

実行結果

良品

良品画像1良品画像2

不良品

不良品画像1不良品画像2

結果

良品1

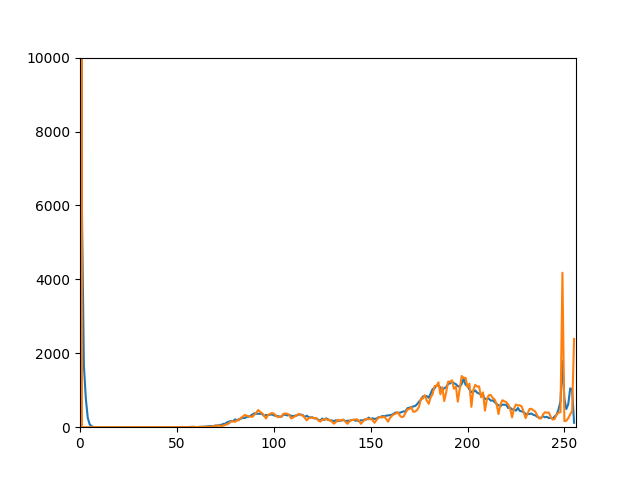
ピアソンの積率相関係数0.96786333

ピアソンの積率相関係数0.96786333

良品2

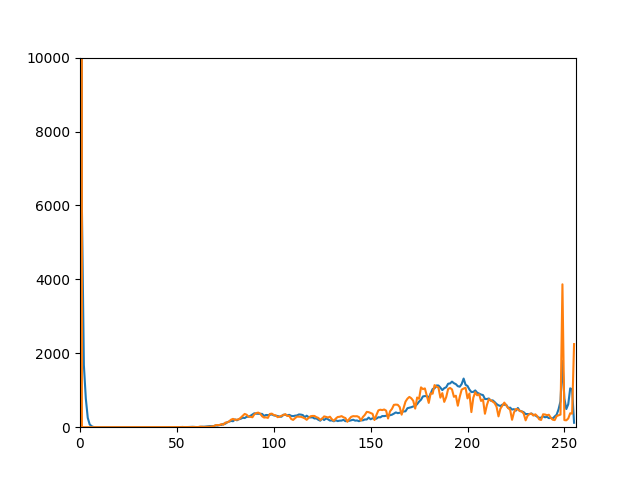
ピアソンの積率相関係数0.93289374

ピアソンの積率相関係数0.93289374

不良品1

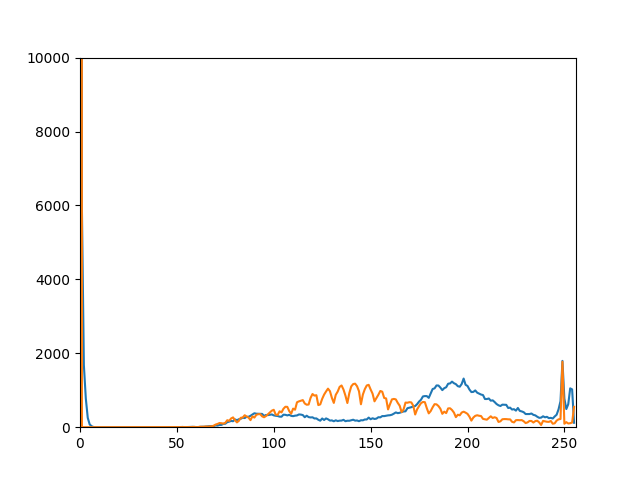
ピアソンの積率相関係数0.19392566

ピアソンの積率相関係数0.19392566

不良品2

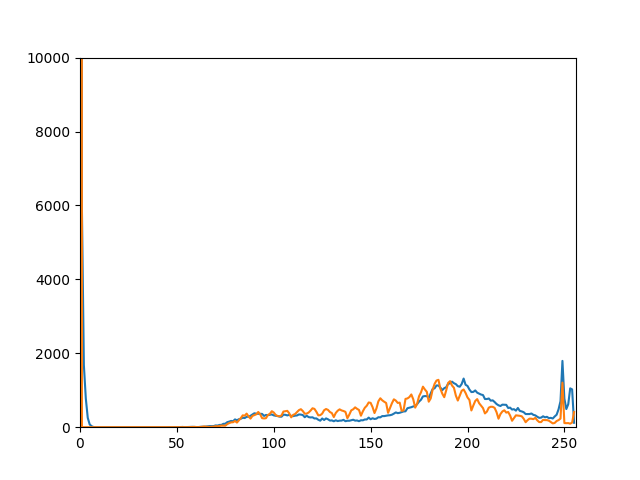
ピアソンの積率相関係数0.8475643

ピアソンの積率相関係数0.8475643

考察

大体うまくいってるように思いますが、不良品2と良品の相関係数が結構近いのが気になります。
画素値的には不良品2は良品に近いようです。
また、検体をどこに置くかによって光のあたり具合も微妙に変わり、相関係数がぶれるようです。
良品と不良品の閾値を厳しめに設定してやって、試運用で調整していくしかなさそうです。
試運用の中で画像を集めてMachine Learningアプローチもとってみようかしら・・・

まとめ

  • 機材を適切に選定して、金属製品ならではの問題を解決した
  • ヒストグラムを用いてメッキ不良の検出を試みた
  • 良品と不良品の閾値は要調整

以上です！