Top Coderとは?
前回の記事を参考にどうぞ。
初参戦 - Single Round Match #727 -
2018/1/11(木)にTop CoderのSingle Round Match #727に初参戦しました。
結果としてはLevel1の問題で229.57 Points獲得しましたが、Level2はテストが通ってSubmitはできたものの、チャレンジで撃墜されました。Level3は難しくて解けませんでした。
TopCoderの問題文と私の解答コードはGitHub上で公開しました。
時間を見つけて復習、修正を行いたいと思います。
初参戦の感想
競技プログラミングは文字列の操作が多そうだという印象がありそうだったので、言語はPythonを選択してみたのですが、Pythonのコレクションクラスのメソッドをよく知らず、リファレンス検索に結構時間を喰ってしまったのが痛かったと思います。
コレクションクラスは基本中の基本となるクラスなので、どんな関数があるか見てみようと思いました。
あとは探索のアルゴリズム等をほぼ忘れてしまっているので復習が必要ですね。
問題について
Level1
AからZで構成された文字列から1文字だけ抜いて、ある文字を連続させることができるなら'Possible'を、どの文字を抜いても連続させることができなかったらImpossibleを返せという問題でした。
私の解答は以下になります。
def solve(self, S):
for i in range(len(S)):
x = S[0:i] + S[i+1:]
prev = ''
for c in x:
if c == prev:
return 'Possible'
prev = c
return 'Impossible'私は全探索で問題を解いていますが、(S[i] == S[i + 1] and len(S) >= 3) or S[i] == S[i + 2]を満たすSであれば'Possible'を返す、という方法でやっている方が多かったように思います。
問題文の条件でSの長さはたかだか50文字と決まっており、僕のやり方でも問題ないのですが、他の方のやり方の方が効率が良いですね。
Level2
問題でいくつかxy平面上の点が与えられ、45度に傾いている2本の直線を使って最大何点を通すことができるでしょうかという問題でした。
def maxPoints(self, x, y):
max = 0
for i in range(len(x)):
b1 = y[i] - x[i]
for j in range(len(x)):
if i == j:
continue
b2 = y[j] + x[j]
t = 2
l = [i, j]
for k in range(len(x)):
if k == i or k == j:
continue
bk1 = y[k] - x[k]
bk2 = y[k] + x[k]
if (bk1 == b1 or bk2 == b2) and (k not in l):
l.append(k)
if len(l) > max:
max = len(l)
return max45度に傾いた直線はy = x + b1とy = -x + b2で表されます。
ここで、y = x + b1はb1 = y - x、y = -x + b2はb2 = y + xと変形できます。
つまり y + xやy - xが等しい値となる点同士が同一直線状になるということになります。
私の解答は、まず2点決定し、それぞれを通る直線を決定した上で、他の点があと何個直線上に乗るか、という考え方です。
このコードは答え自体問題ないのですが、実行時間でアウトです。
x, yが共に長さ1000のタプルである場合、実行時間は2.531sとなり、制限時間の2.000sを上回ってしまいました。
チャレンジでこれを試されたのでしょうが、実行時間系ってやっぱりちゃんとステップ数計算してからチャレンジするんですかね?
3重構造にしてるからまずいのでしょうね。
3重を2重x2に分解できそうなので、やってみようと思います。
2018/01/13追記
とりあえず3重ループを2重ループに直すことができました。
class TwoDiagonals:
def maxPoints(self, x, y):
N = len(x)
A = {}
B = {}
AB = {}
Xs = []
Ys = []
for i in range(N):
X = x[i] - y[i]
Y = x[i] + y[i]
A[X] = A.get(X, 0) + 1
B[Y] = B.get(Y, 0) + 1
AB['{},{}'.format(X, Y)] = AB.get('{},{}'.format(X, Y), 0) + 1
if X not in Xs:
Xs.append(X)
if Y not in Ys:
Ys.append(Y)
res = 0
for i in Xs:
for j in Ys:
res = max(res, A.get(i, 0) + B.get(j, 0) - AB.get('{},{}'.format(i, j), 0))
return res最初のループで各点のx - yとx + yの値を求めて、その値を持つ点の個数を数えます。
また、各点ごとにx - yとx + yの値のペアをキーとして、1という値を入れておきます。
前準備が終わったら2重ループで、どの組み合わせが一番大きくなるかを探索してます。
下の式でAB.get('{},{}'.format(i, j), 0)が0でない場合(1である場合)というのは、2本の線の交点に入力として与えられた点が存在する場合です。A.get(i, 0) + B.get(j, 0)だけでは1つ余分にカウントしてしまっている状態なので、その分を引いています。
max(res, A.get(i, 0) + B.get(j, 0) - AB.get('{},{}'.format(i, j), 0))これで、与えられたテストは通ったので、あとは実行時間を測るために入力としてX = [1, 2, ..., 1000]とY = [1, 2, ..., 1000]を与えてみます。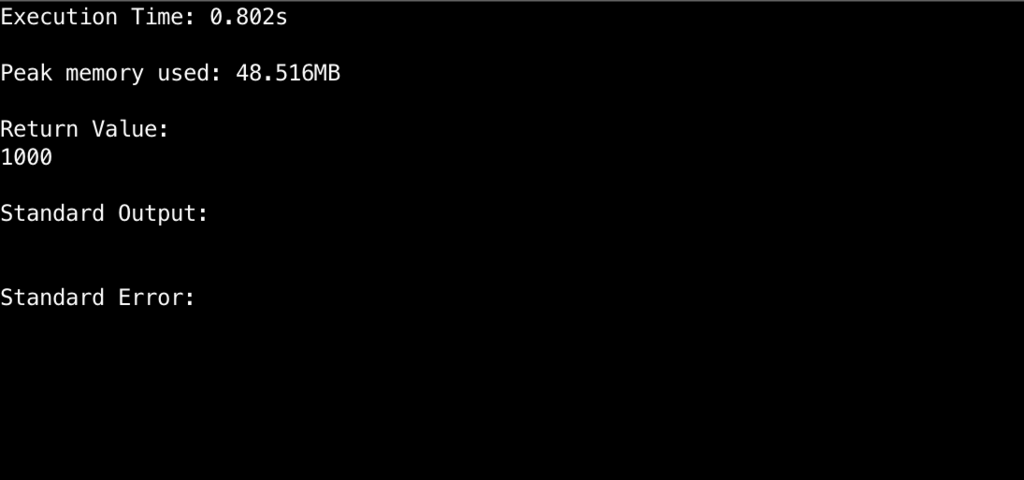
実行時間もかなり余裕がありますね。
Level3
問題を説明するのが難しいので、そのまま載せます。
Definition: for two strings X and Y, we say that a string X has a subsequence Y if and only if it's possible to remove 0 or more characters in X so that the remaining characters form the string Y. For example, "ABCDEFFF" has subsequences "B", "ABFF" and "ABCDEFFF", but doesn't have subsequences "XSFJ", "BA" and "CCDD".
Limak has a string S that consists of uppercase English letters ('A' - 'Z'). He can add more characters (also uppercase English letters) in S. For example, if S is "ABXB", he can get "BAOUBXBB" by inserting 'B', 'O', 'U' and 'B'.
You are given three strings S, A and B, each consisting of uppercase English letters. Limak wants to add characters anywhere into S, including its beginning and end, so that the new string has the subsequence A but doesn't have the subsequence B. Find and return the minimum possible number of added characters. If Limak can't obtain a string with the desired properties, return -1 instead.解答に関しては私はわかりませんでしたので、分かり次第追記します。